On Window TinyLFU

I was first introduced to the Window TinyLFU algorithm through a wiki entry for the caffeine project.

The graphs looked neat, but it took actually reading the Einziger and Friedman paper, TinyLFU: A Highly Efficient Cache Admission Policy to understand just how interesting and simple the algorithm actually is. Unlike many papers in computer science, this one is extremely consumable for those (like myself) lacking a strong math background.

I’ve been studying this algorithm with interest, since it is quite relevant to my work at Fastly. I’ve a few ideas for possible extensions, as well as some for efficient lock-free implementations. But first, let’s talk about cache eviction and how TinyLFU works.

LRU?

Why not just use LRU and be done with it? There are a few practical problems with LRU:

• LRU is not scan resistant. What this means is that, given a cache of N items, an attacker can send N+1 requests in sequence. Once an initial scan is completed, all subsequent scans will result in cache misses.
• Every hit requires moving objects in the queue. When queues are dynamically allocated, this results in high cache miss overhead, TLB thrashing, and memory writes.
• With high request loads comes high lock contention.

Because of these problems, LRU implementations frequently employ clever tricks to reduce lock contention. This can be achieved with a few strategies:

• Don’t promote items that were recently promoted. (They’re probably still near the front of the LRU.)
• Don’t promote items in the face of lock contention.

Under high load, these strategies (coupled with the lack of scan resistance) combine in a way that results in dropping items that have some regular access frequency. These are items that we always want to have cached – so shouldn’t we consider usage frequency as part of our caching strategy?

LFU Background

Access frequency seems like a good thing to use as a cache eviction strategy. It even seems like a pretty close approximation to the clairvoyant algorithm: cache every item that is frequently used.

Easier said than done.

Aging

The first problem is one of aging. Frequency isn’t a useful absolute metric in terms of knowing which objects are worth keeping. This is especially true for sites like Imgur, where front-page images will see many impressions on one day, and then effectively never be accessed again. To address this, we need some method of aging hit counts. This means that over time, the weight of a hit decreases by some factor.

How do we determine how often to age? How do we determine a good weight to use?

The Squid proxy provides links to a couple papers at their cache_replacement_policy documentation that describe two approaches used for aging when using frequency as a cache metric.

Memory Overhead

Keeping an access frequency on cached objects is common. To effectively use a frequency-based caching strategy, we also have to remember the access frequency of objects we no longer have in cache. In a system that sees and forgets about billions of distinct objects per day, the memory overhead of maintaining counters is not tenable.

Some approaches to solving this include the use of saturating counters. (A saturating counter is a counter that increments up to, but not past, some maximum value.) If we assume that any object with a frequency larger than X is an object that we want to cache, we might be able to reduce our counter space. But by how much? 1 byte only gives us 256 values (assuming CHAR_BIT is 8). What about 2 bytes? If we see 2 billion distinct objects per day, we end up using 28GB of memory just to hold counters after a week of uptime. This is memory that we cannot use to actually cache objects.

Admission

LFU is sometimes implemented as a cache admission policy, not an eviction policy. What this means is that when a cache lookup results in a miss, and the resolution of the miss results in storing a cacheable item, that item does not become cached until it surpasses some access frequency. For example, if every cached item has a access frequency of (say) at least 100 per aging period, this new item will effectively result in a miss every time until its access frequency meets or exceeds this threshold.

We typically solve this problem by creating a “window” cache in front of the LFU that caches low frequency items using some simpler approach, like an LRU. When items from the window cache are evicted, their access frequency during their time in the windowed cache is compared to their LFU frequency count to determine whether or not these items should be inserted into the main cache.

TinyLFU

These problems are hard to address, but given the promise of LFU, much research has gone into solving them. Enter TinyLFU. TinyLFU provides means for solving the problems of aging and memory overhead. In a subsequent paper, Ben Manes introduces Window-TinyLFU, which solves what it terms the “sparse burst” problem where repeated access to a new object results in many cache misses.

Dealing with Aging

First, we should consider the novel way TinyLFU handles aging. To keep frequencies “fresh”, a counter is maintained that attempts to target the sample size. The sample size is effectively the period at which we age. This period is not duration based, but is instead measured on incoming requests. The paper refers to this as W. (The paper tries very hard not to confuse the reader about the term window, but I was too dense to not be confused for a period of months.)

When this counter reaches the sample size (W), both the counter and all frequency sketches are divided by two. The paper goes on to prove that the error bounds resulting from integer divisions are reasonable and maintain a level of correctness desired from such a structure.

This division operation surprisingly simple (at least moreso than sliding window-based strategies), and usually rather efficient on modern processors.

Solving Memory Overhead

As we explored in the previous section, simply reducing counter size is not sufficient to reduce memory overhead to a usable amount. TinyLFU makes a novel observation about cache frequency patterns that not only allows us to drastically reduce counter size to under one byte, but also employs probabilistic algorithms to reduce the total number of counters we must store.

Reducing the Number of Counters

The first novel suggestion made by the paper is to reduce the number of counters by using probabilistic algorithms. This can be done by using an approximate count; section 2.2 of the paper details a number of possible schemes for this, but in this post, I will focus on discussing what is called a “minimal increment counting Bloom filter”.

Minimal Increment Counting Bloom Filters

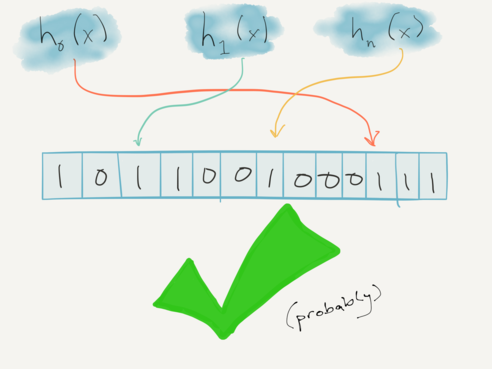
Bloom filters are probabilistic data structures that can be used to determine whether some item is a member of some set. Instead of storing the entire set of items, a Bloom filter relies on computing several hashes of the items in a set. The result of this hash is used as an index into a bit set – if the bit is set, the item is probably in the set. If it is not set, the item is definitely not in the set. By increasing the number of distinct hash functions calculated on the elements, and increasing the total bit space, we can increase our certainty of whether the item is actually a member of the set on a hit.

For instance, using N hash functions, this lookup means the item is probably in the set:

This lookup means the item is definitely not in the set:

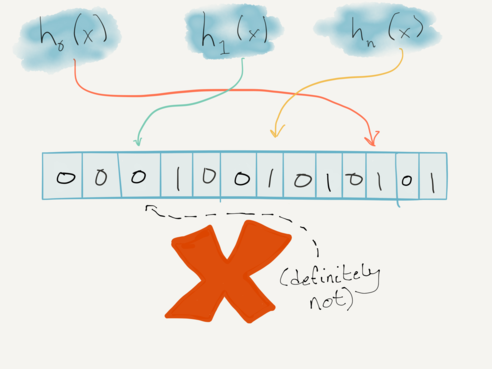
But Bloom filters can say more than just “probably” and “definitely not”. A “counting Bloom filter” can keep track of counts (in fact, the standard Bloom filter could be considered a 1-bit counting Bloom filter). In this case, each element in the Bloom filter space represents a (possibly saturating) counter.

The problem with this is that multiple items share counters. To keep our counters small, we need a means of making sure counters shared between objects with wildly different access frequencies do not skew each other too much. This is where the “minimal increment” counters come into play. Effectively, this structure only increments the smallest counters by one.

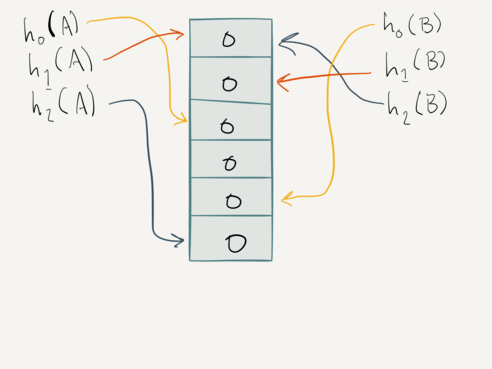
Let’s visualize this. All counts start off at zero. And let’s assume we have two items for which to track access frequency. At the beginning we have a set of distinct, zeroed counters {0, 0, 0, 0, 0, 0}:

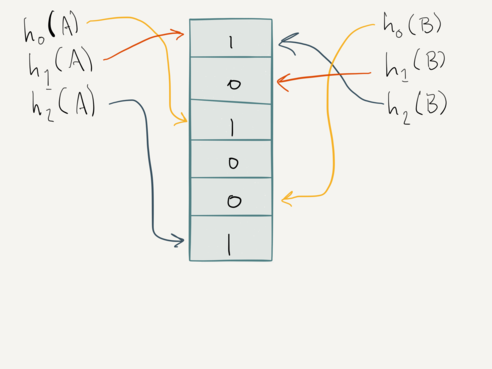
After we record a hit on item A, we increment its smallest counters by one. Since all counters are zero, the counters for item A become {1, 1, 1}, and the total set becomes {1, 0, 1, 0, 0, 1}:

Once we record a hit on item B, we increment only its smallest counters – but note that it shares a counter with item A. Therefore, we only increment the two non-shared counters. Item B’s counters also become {1, 1, 1}, and the total set becomes {1, 1, 1, 0, 1, 1}:

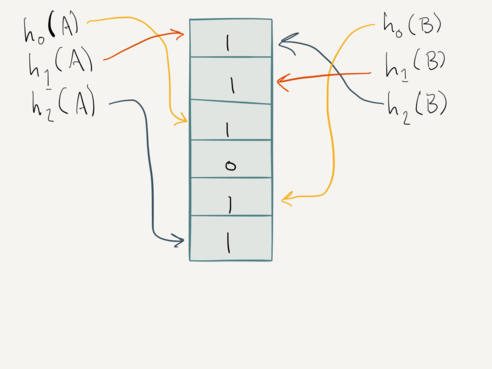
If we had initially had three hits on A, its counters would be {3, 3, 3}; the total state would be {3, 0, 3, 0, 0, 3}. The counters for B would be {0, 0, 3}. Because we only ever increment or use the least of the counters, item B still has a hit rate of 0!

Using a probabilistic data structure (like a Bloom filter) for this purpose is ideal; it has predictable bounds of error, and it significantly reduces the total number of counters we need. (For more on probabilistic algorithms and data structures, I highly recommend Tyler McMullen’s talk, It Probably Works.)

Reducing Size of Counters

We already saw how reducing counters to even 1 byte can be cost prohibitive. With our Bloom filter, we significantly reduce the total number of counters we need. But we can still save more. Citing my favorite observation from the paper:

…a frequency histogram only needs to know whether a potential cache replacement victim that is already in the cache is more popular than the item currently being accessed. However, the frequency histogram need not determine the exact ordering between all items in the cache.

Because the aging policy of TinyLFU resets all counters simultaneously (instead of using e.g. a sliding window), and because of this observation that we only care about the popularity of an individual item with respect to the popularity of all cached items (irrespective of their ordering), we get another nice space savings win.

Using this information, the draws two conclusions:

[Given] a cache of size C, all items whose access frequency is above 1/C belong in the cache (under the reasonable assumption that the total number of items being accessed is larger than C).

This statement took me months to understand.

We have a cache sized to C, but this size is (potentially much) smaller than the total set of items S that could be accessed through it (as is true for many applications of a cache). So C is smaller than S.

Let’s assume that we have N requests for M distinct objects over some time period. It doesn’t matter what the time period is. Any distinct item I requested within our N requests, may have been requested more than once. D is what we’ll call the number of times I was requested during this sample. What this statement says is when D/N is larger than 1/C, the item I should be cached.

But it turns out that our aging factor gives us a time period in terms of number of requests already! We sample our frequency counts based on this number W. So now we get this really great caching rule:

Cache I when D/W is larger than 1/C.

But wait! This means that we don’t actually care about D, just the relationship between the ratios. This means that we can cap our counters at W/C. Since W is somewhat arbitrarily defined (a larger sample size increases accuracy of the frequency histogram with respect to the frequency of any individual cacheable item), this also means we get to say how much space we want to waste. The paper elightens us to the space savings:

To get a feel for counter sizes, when W/C = 8, the counters require only 3 bits each, as the sample is 8 times larger than the cache itself. For comparison, if we consider a small 2K items cache with a sample size of 16K items and we do not employ the small counters optimization, then the required counter size is 14 bits.

This choice also affects the number of counters we need to keep track of. In particular: if you define W as 8C, you only need to keep enough counters to represent the number of distinct object accesses you have across 8C requests. If your cache size is something around 100 million objects, you only need to care about the average uniqueness of 800 million requests. This is usually something you can measure.

The Doorkeeper

Especially in HTTP caches, long-tail objects account for a large portion of cacheable content. These are objects that are usually pretty low frequency, but live forever. Furthermore, such items will usually only get a single hit (if any) within the sample time. Why should we keep around “fat” counters for items that rarely see hits?

The Doorkeeper solves this problem: it is a single-bit minimum-increment counting Bloom filter. Any incoming requests for items must pass the Doorkeeper before being promoted to fat counters, effectively allowing us to use fewer fat counters than we would otherwise need: a double savings.

Once we have all these bits in place, we can simply couple this algorithm to whichever cache we choose – be it LRU, ARC, SLRU, 2Q, or whatever else floats your fancy.

Wrapping Up

We’ve looked at the components of TinyLFU, and discussed how Window TinyLFU solves a number of issues that have prevented practical use of LFU strategies for large caches.

I’ll be following this post up in the next couple months with some implementation approaches. I have an interesting (but maybe obvious) idea to do with promoting items from the window cache to the main cache, which I’d like to explore. I also have some ideas on how this can be implemented in a lock-free fashion, which is critical for caches with highly concurrent workloads. There are also a few optimizations that can be made around things like the Doorkeeper.

After that, we’ll take a look at some experimental results. The paper presents some results, but I’d like to take a look at how this works on gigantic data sets.